球谐函数

直观了解

参考文章：https://zhuanlan.zhihu.com/p/351289217
球谐函数可以类比泰勒展开，傅里叶级数。都是通过一组不同阶的基函数线性组合而成，只不过傅里叶级数的基函数是三角函数，而球谐函数的基函数是球函数。即正交基为球函数，极坐标即球函数系数。

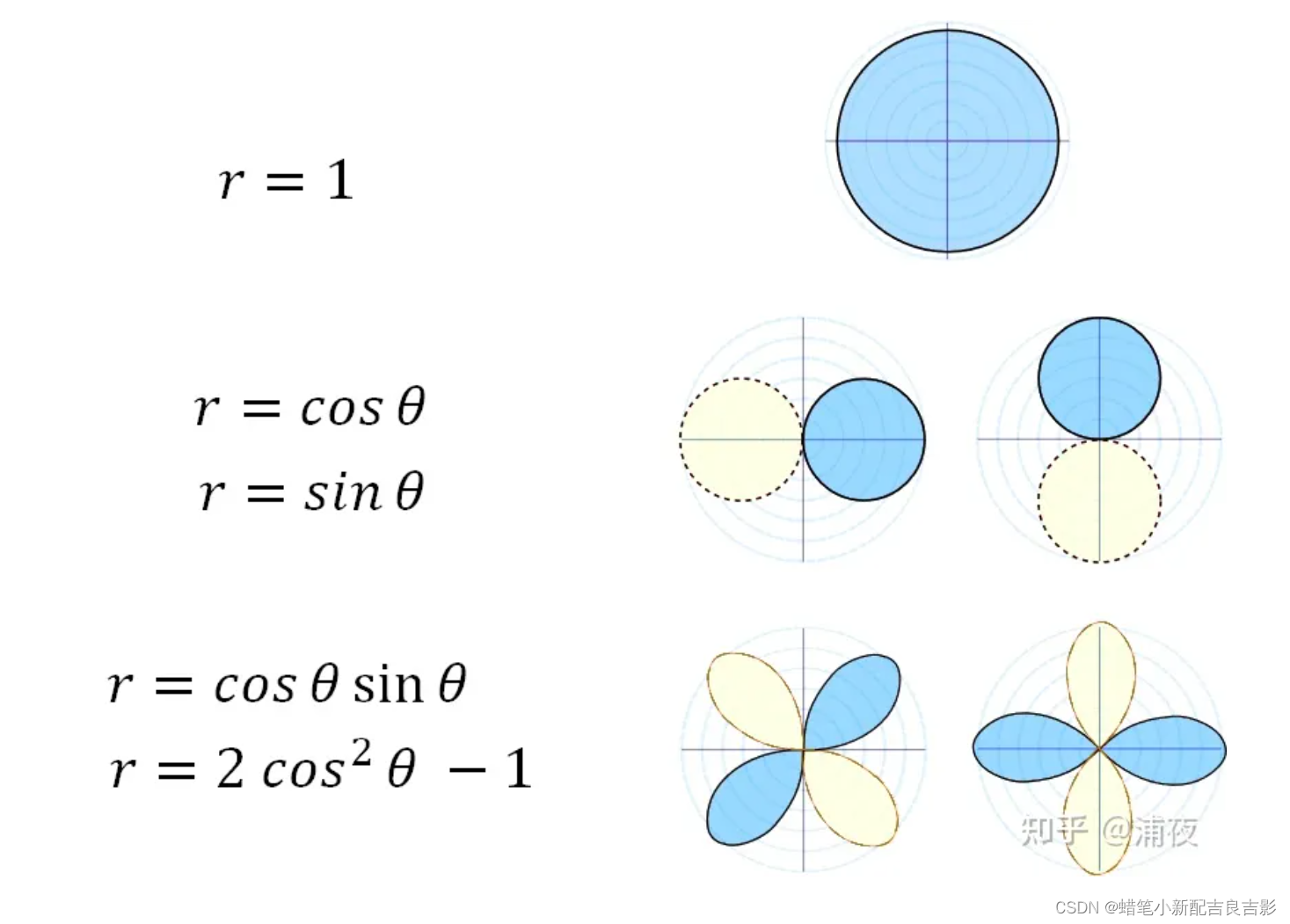
同样就像傅里叶变换拟合曲线一样，球谐函数拟合3d物体时，所用阶数越高，拟合越贴切，但是也有可能出现过拟合的情况。

球谐函数性质

1. 正交性：各个基函数之间线性独立
2. 旋转不变性：环境光照变化之后只需要简单的计算就可以得到光源旋转之后的结果，在后续应用中补充。

若将函数所表示的距离变成颜色上的数值差异，就可以用球谐函数来拟合颜色信息。

球谐光照

参考文章：

1. https://zhuanlan.zhihu.com/p/359856625
2. https://zhuanlan.zhihu.com/p/363600898

漫反射光照函数
$$L(p,w_o)={\int }_{\Omega }L(p,{\omega }_i)n\cdot {\omega }_{i}d{w}_i$$

• $\Omega$为半球空间,入射光方向 $w_i$,观察方向 $w_o$,着色点$p$,$n$ 为着色点 $p$ 的法线。

进行替换
$$\{\begin{array}{rl}& light(w)=L(p,w)\\ & t(w)=n\cdot w\end{array}$$

进行球谐函数展开
$$\{\begin{array}{rl}& light(w)=\sum _{i=0}{L}_i{Y}_i(w)\\ & t(w)=\sum _{i=0}{t}_i{Y}_i(w)\end{array}$$
带回光照函数模型化简
$$L(p,w_o)=\sum _{i=0}{L}_i{t}_i$$
此时形式简单，但是实际上计算时，需要预计算$t_i$，即对每一组法线方向都要计算一组球谐函数得到其系数，实际开销较大。于是利用球谐函数旋转不变性的性质继续推导得到
$$L(n)=\sum _{l=0}^{\infty }\sum _{m=-l}^l\sqrt{\frac{4\pi }{2l+1}}{L}_l^m{t}_l{Y}_l^m(n)$$
此时只需要通过顶点着色器传入的法向量n计算出球谐函数$Y_l^m(n)$，再与常数相乘，不需按原来要对每个t都单独通过积分求解。