白盒 AES 实现方式

白盒算法的核心思想是将密钥信息混淆到算法中，让攻击者无法解析出算法的内部细节，也无法还原出密钥的一种算法(实际上还是有方法的)。

通常来说白盒AES的实现有三种方式：Chow等人的查找表方式、Bringer等人的插入扰乱项的方式、Biryukov等人的多变量密码的方式，下面进行简单的介绍三种方式：

01. 查找表技术

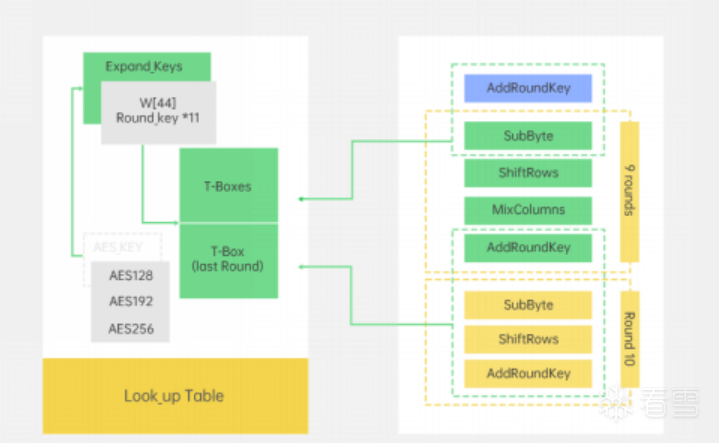
查找表技术是由Chow等人在论文《White-Box Cryptography and an AES Implementation》中最早提出的白盒加密技术方案，可基于DES或AES等分组密码算法实现，属于标准密码算法白盒化范畴。

任何有限函数理论上都可转化为一个包含所有可能的输入和输出的查找表。举一个极端的例子，如果将AES-128加密用一个简单的查找表来表示，即先将128比特密钥固定，每种可能的128比特明文输入（共2^128种可能）一一对应了一种128比特密文输出，那么AES-128可以用一个5.4×10^39字节（2^128×128比特）的查找表替换。

核心思想是针对给定的密钥，把 AES 运算过程的每一轮操作拆分成一个个小模块，之后对每个模块进行混淆置乱编码， 最后将每个模块所有可能的输入输出做成一个查找表，用查找表来表示这些模块。白盒 AES 的算法执行过程就等效转换成对一个个查找表进行查找的过程。

攻克：

在 2004 年，Billet 等人在论文《Cryptanalysis of a White Box AES Implementation》中提出了一个非常有效的 BGE 攻击方法， 他们选择某些特定的查找表，合并成一个可以用输入输出表示的函数，使用代数的方法去掉其中的非线性部分，提取出隐藏在T-Box 中的密钥。这个攻击在 2008 年由 Michiels 等人改进为一种通用攻击方法《Cryptanalysis of White-Box Implementations》，可以对类似算法的白盒实现进行攻击。2013 年 Lepoint 等人在《Another Nail in the Coffin of White-Box AES Implementations》中提出了一种更加有效的攻击方法，能够以 2的22次方复杂度恢复 AES 的密钥。

02. 插入干扰项

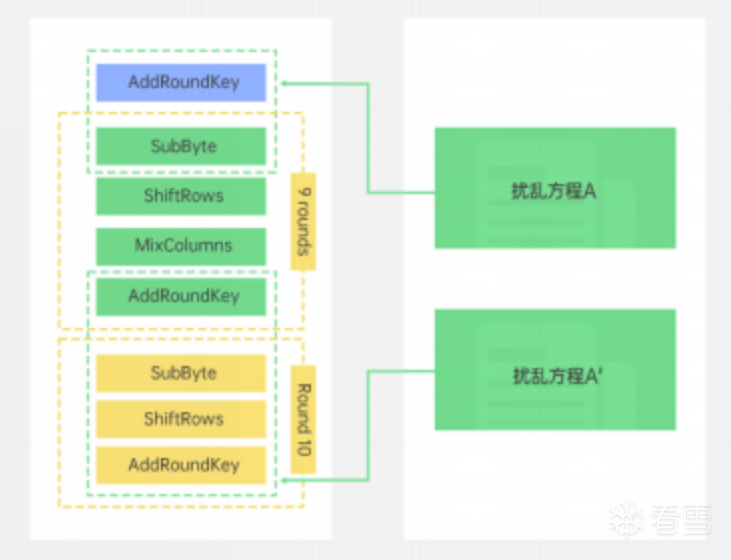
2006 年 Bringer 等人中提出一个新 AES 白盒实现方法《White Box Cryptography: Another Attempt》，该方法使用同构多项式问题。其主要思想是通过增加额外的扰乱方程和线性编码，成功扰乱了原始的代数结构，增强了白盒实现的安全性，从而使得针对代数结构进行的攻击变得困难。

攻克：

2010 年 Mulder 、Roelse 和 Preneel提出了一种针对 Xiao 和 Lai 提出的白盒 AES 实现的攻击方法《Cryptanalysis of the Xiao-Lai White-Box AES Implementation》，攻击方法的核心是通过分析白盒实现中的查找表和编码关系，提取出隐藏的密钥信息，能够以较低的复杂度恢复出等价密钥。

03. 多变量密码

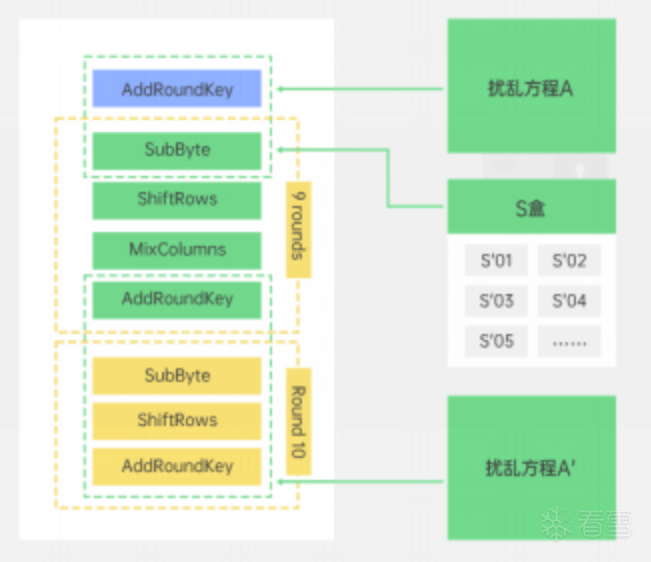
在各种白盒实现方案被相继攻破之后, 2014 年, Alex Biryukov 等人提出基于 ASASA 结构的通用白盒密码设计方法《Cryptographic Schemes Based on the ASASA Structure: Black-Box, White-Box, and Public-Key》。这种设计方式通过插入扰乱项和扩展 S 盒，分为强白盒密码设计和弱白盒密码设计两类，成功增强了白盒实现的安全性。

ASASA 结构

• ASASA 结构是一种通用的密码设计框架，由两个仿射变换（Affine）和一个非线性变换（S-box）交替组成。
• 具体结构为：Affine → S-box → Affine → S-box → Affine。
• 这种结构可以用于设计对称密码、公钥密码和白盒密码。

强白盒密码设计

• 强白盒密码设计的目标是保护密钥的安全性，即使攻击者能够完全访问加密代码和中间计算结果。
• 作者使用有限域上的多变量多项式的方法，分别以 χ-scheme 和扩展 S 盒（expanding S-box）来实现 ASASA 中的 S 盒。
  • χ-scheme: 使用有限域上的多变量多项式来实现 S 盒，增加了非线性混淆。
  • 扩展 S 盒: 通过扩展 S 盒的输入输出维度，进一步增加混淆的复杂性。
• 这两种方案都需要插入扰乱项来抵抗攻击。

弱白盒密码设计

• 弱白盒密码设计的目标是保护密钥不被发现和推导，但无法完全防止攻击者通过分析查找表来恢复密钥。
• 弱白盒设计通常使用较小的查找表和简单的混淆技术，适用于资源受限的环境。

攻克：

ASASA 结构（Affine-Sbox-Affine-Sbox-Affine）通过交替的仿射变换和非线性变换（S-box）来隐藏密钥和加密逻辑。然而，这种结构在某些情况下仍然可能被攻破，特别是当攻击者能够利用其代数特性或统计特性时，针对 ASASA 结构的攻击方法主要有以下几种：

代数攻击

• Gröbner 基攻击：ASASA 结构中的非线性变换（S-box）和仿射变换可以被建模为多项式方程组。攻击者可以使用 Gröbner 基算法来求解这些方程组，从而恢复密钥或加密逻辑。
• 线性化攻击：通过分析 ASASA 结构中的线性层，攻击者可以尝试将非线性部分线性化，从而简化攻击过程。

统计攻击

• 差分攻击：攻击者可以通过分析输入输出的差分特性，推断出 ASASA 结构中的非线性变换和仿射变换的具体形式，从而恢复密钥。
• 积分攻击：通过分析查找表输出的统计特性，攻击者可以推断出密钥信息。例如，某些 ASASA 实现中，查找表输出的中间值可能存在统计规律，攻击者可以利用这些规律进行积分攻击。

分解攻击

• 结构分解：ASASA 结构的多层变换可能被分解为更简单的组件，攻击者可以通过分析这些组件的特性，逐步恢复密钥或加密逻辑。

后续的研究者提出了多种攻击方法，揭示了该结构的潜在弱点，感兴趣的可自行查阅：

• Cryptographic Schemes Based on the ASASA Structure
• WAS: Improved White-Box Cryptographic Algorithm

查找表方案的白盒AES实现过程

基于查找表实现方案的理论基础已经有很多详细且成熟的文章，其中部分文章也提供代码参考，在此不做过多赘述，读者可自行阅读以下文章(建议先阅读至少一两篇再回来)：

• 128位AES算法加密、解密文件流程及C语言实现

• 【密码学】一文读懂白盒AES(Chow方案)(一)

• AES白盒加密解读与实现（Chow方案）

• Differential Fault Analysis on White-box AES Implementations

通过以上文章的分析，我们将加密流程拆分成以下的过程：

• 通过TBoxes 实现 AES 的 SubBytes 和 AddRoundKey
• 通过 TyiTableBoxes 实现 AES 的MixColumns
• 通过 shiftTab 数组实现 AES 的ShiftRows

接下来我们分步骤来具体实现一下的流程。

01. 密钥扩展

首先必不可少的是密钥扩展算法，将初始密钥扩展为 176 字节的轮密钥，轮密钥是后续流程的基础，提供expandedKey函数以供参考：

• 初始密钥的前 16 字节直接复制到 expandedKey 中。
• 后续的轮密钥通过前一轮的轮密钥和 S 盒（sBox）生成。
• 每 4 轮使用轮常数（rCon）进行异或操作，确保轮密钥的唯一性。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42

void expandKey(const u8 *key) {     u8 tmp[4]; // 临时数组，用于存储每一轮的轮密钥     unsigned i, j; // 循环变量       // 第一步：将初始密钥的前 16 字节（128 位）直接复制到 expandedKey 中     for (i = 0; i < 4; i++)     {         expandedKey[4 * i] = key[4 * i];         // 复制第 4*i 字节         expandedKey[4 * i + 1] = key[4 * i + 1]; // 复制第 4*i+1 字节         expandedKey[4 * i + 2] = key[4 * i + 2]; // 复制第 4*i+2 字节         expandedKey[4 * i + 3] = key[4 * i + 3]; // 复制第 4*i+3 字节     }       // 第二步：生成后续的轮密钥（共 10 轮，每轮 16 字节，总共 176 字节）     for (i = 4; i < 44; i++)     {         // 获取上一轮的轮密钥的最后 4 个字节         j = (i - 1) * 4;         tmp[0] = expandedKey[j];     // 上一轮的第 j 字节         tmp[1] = expandedKey[j + 1]; // 上一轮的第 j+1 字节         tmp[2] = expandedKey[j + 2]; // 上一轮的第 j+2 字节         tmp[3] = expandedKey[j + 3]; // 上一轮的第 j+3 字节           // 每 4 轮进行一次特殊处理（即 AES 密钥扩展中的 g 函数）         if (i % 4 == 0)         {             int k = tmp[0]; // 保存 tmp[0] 的值，用于后续的循环移位             // 对 tmp 数组进行循环移位，并通过 S 盒进行非线性替换             tmp[0] = sBox[tmp[1]] ^ rCon[i / 4]; // 第 1 字节替换并与轮常数异或             tmp[1] = sBox[tmp[2]];               // 第 2 字节替换             tmp[2] = sBox[tmp[3]];               // 第 3 字节替换             tmp[3] = sBox[k];                    // 第 4 字节替换         }           // 生成当前轮的轮密钥：将上一轮的轮密钥与 tmp 数组进行异或操作         expandedKey[4 * i] = expandedKey[4 * (i - 4)] ^ tmp[0];     // 第 4*i 字节         expandedKey[4 * i + 1] = expandedKey[4 * (i - 4) + 1] ^ tmp[1]; // 第 4*i+1 字节         expandedKey[4 * i + 2] = expandedKey[4 * (i - 4) + 2] ^ tmp[2]; // 第 4*i+2 字节         expandedKey[4 * i + 3] = expandedKey[4 * (i - 4) + 3] ^ tmp[3]; // 第 4*i+3 字节     } }

02. 通过 TBoxes 实现SubBytes 和 AddRoundKey

SubBytes 操作

• SubBytes 是 AES 的非线性替换步骤，通过 S 盒（sBox）将每个字节替换为另一个字节。
• S 盒是一个固定的 256 字节查找表，定义了每个字节的替换规则。

AddRoundKey 操作

• AddRoundKey 是 AES 的密钥加步骤，将输入数据与轮密钥进行逐字节异或操作。
• 轮密钥是通过密钥扩展算法从初始密钥生成的(01 章节)。

在白盒加密中，SubBytes 和 AddRoundKey 可以合并为一个查找表，称为 TBoxes。TBoxes[i][j][x] 表示第 i 轮、第 j 个字节、输入为 x 时的输出，计算公式为：

1	TBoxes[i][j][x] = sBox[x ^ expandedKey[16 * i + j]] ^ expandedKey[16 * (i + 1) + j]

• x ^ expandedKey[16 * i + j] 实现了 AddRoundKey 操作
• sBox[...] 实现了 SubBytes 操作
• ^ expandedKey[16 * (i + 1) + j] 是下一轮的 AddRoundKey 操作（用于混淆）。

在 TBoxes 中，密钥被嵌入到查找表的生成过程中，攻击者即使能够访问 TBoxes，也无法直接提取密钥，因为密钥已经与 S 盒和随机数据混淆了，下面给到生成 TBoxes 的关键代码：

- ShiftRows: 通过 shiftTab 数组实现

- SubBytes 和 AddRoundKey: 通过 sBox 和 expandedKey 实现，并存储在 TBoxes 中

- 混淆: 使用 ioInvTable 对输入数据进行随机混淆

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

for (int i = 0; i < 10; i++) {     for (int j = 0; j < 16; j++) {         int orgJ = shiftTab[j]; // ShiftRows 操作         u8 ioInv = ioInvTable[orgJ]; // 随机混淆数据         for (int x = 0; x < 256; x++) {             u32 tmp = x;             if (i != 0)                 tmp = tmp ^ ioInv; // 混淆输入             tmp = sBox[tmp ^ expandedKey[16 * i + orgJ]]; // SubBytes 和 AddRoundKey             TBoxes[i][j][x] = tmp;                         ...         }     } }

03. 通过 TyiTableBoxes 实现MixColumns

MixColumns 是 AES 加密中的一个线性变换步骤，它对状态矩阵的每一列进行变换，每一列的 4 个字节通过矩阵乘法与一个固定的矩阵（称为 MixColumns 矩阵）进行运算。MixColumns 操作可以表示为以下矩阵乘法：

1 2 3 4

| c0' |   | 02 03 01 01 |   | c0 | | c1' | = | 01 02 03 01 | * | c1 | | c2' |   | 01 01 02 03 |   | c2 | | c3' |   | 03 01 01 02 |   | c3 |

- c0, c1, c2, c3 是输入列的 4 个字节。

- c0', c1', c2', c3' 是输出列的 4 个字节。

- 矩阵中的元素（如 02、03）是有限域 GF(2^8) 中的乘法系数。

在白盒化的过程中，MixColumns 操作通过 TyiTableBoxes 来实现，TyiTableBoxes 的值直接从 TyiTables 中获取，TyiTables 已经预先计算了 MixColumns 的结果。

其中TyiTables 是一个 16x256 的查找表，生成过程大致如下：

1 2 3 4 5 6 7 8 9 10 11 12

for (int j = 0; j < 4; j++) {     for (int x = 0; x < 256; x++) {         TyiTables[4 * j + 0][x] =             ((gMul(2, x) ^ ioInvTable[4 * j + 0]) << 24) | (x << 16) | (x << 8) | gMul(3, x);         TyiTables[4 * j + 1][x] =             (gMul(3, x) << 24) | ((gMul(2, x) ^ ioInvTable[4 * j + 1]) << 16) | (x << 8) | x;         TyiTables[4 * j + 2][x] =             (x << 24) | (gMul(3, x) << 16) | ((gMul(2, x) ^ ioInvTable[4 * j + 2]) << 8) | x;         TyiTables[4 * j + 3][x] =             (x << 24) | (x << 16) | (gMul(3, x) << 8) | gMul(2, x) ^ ioInvTable[4 * j + 3];     } }

- gMul 函数实现了有限域 GF(2^8) 中的乘法

- ioInvTable 是一个随机混淆数据

- TyiTables 的每个表项是一个 32 位整数，包含了 MixColumns 操作的结果

有了TyiTables之后，我们来看一下TyiTableBoxes的具体逻辑，TyiTableBoxes 是一个 9x16x256 的查找表，用于替换 MixColumns 操作。它的生成过程如下：

TyiTableBoxes[i][j][x] 表示第 i 轮、第 j 个字节、输入为 x 时的 MixColumns 操作结果

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

for (int i = 0; i < 10; i++) {     for (int j = 0; j < 16; j++) {         int orgJ = shiftTab[j];         u8 ioInv = ioInvTable[orgJ];         for (int x = 0; x < 256; x++) {             u32 tmp = x;             if (i != 0)                 tmp = tmp ^ ioInv;             tmp = sBox[tmp ^ expandedKey[16 * i + orgJ]];             TBoxes[i][j][x] = tmp;             if (i == 9) {                 TBoxes[i][j][x] ^= expandedKey[160 + j];             } else {                 TyiTableBoxes[i][j][x] = TyiTables[j][tmp]; // MixColumns 操作             }         }     } }

MixColumns操作是 AES 算法的核心步骤，查分故障分析也是从该操作入手进行密钥还原攻击，在TyiTables生成的过程中我们添加了ioInvTable进行混淆，除此之外我们还可以在TyiTableBoxes的标准化过程中添加混淆矩阵来进一步干扰：

1 2 3 4 5 6 7 8 9 10

for (int i = 0; i < 9; i++) {     for (int j = 0; j < 4; j++) {         for (int x = 0; x < 256; x++) {             TyiTableBoxes[i][4 * j + 0][x] ^= MixTable[x % 16];             TyiTableBoxes[i][4 * j + 1][x] ^= MixTable[x % 16];             TyiTableBoxes[i][4 * j + 2][x] ^= MixTable[x % 16];             TyiTableBoxes[i][4 * j + 3][x] ^= MixTable[x % 16];         }     } }

04. 通过 shiftTab 数组实现ShiftRows

最后就是 shiftRows的实现过程了，ShiftRows 是 AES 加密中的一个步骤，它对状态矩阵的每一行进行循环移位，具体来说：

• 第 0 行不移位。
• 第 1 行向左循环移位 1 个字节。
• 第 2 行向左循环移位 2 个字节。
• 第 3 行向左循环移位 3 个字节。

假设状态矩阵为：

1 2 3 4

| a0 a1 a2 a3 | | b0 b1 b2 b3 | | c0 c1 c2 c3 | | d0 d1 d2 d3 |

经过 ShiftRows 操作后，状态矩阵变为：

1 2 3 4

| a0 a1 a2 a3 | | b1 b2 b3 b0 | | c2 c3 c0 c1 | | d3 d0 d1 d2 |

在白盒化的过程中，ShiftRows 操作通过 shiftTab 数组来实现，shiftTab 数组定义了 ShiftRows 操作的字节位置映射。它的定义如下：

1 2 3 4 5 6

int shiftTab[16] = {     0, 5, 10, 15, // 第 0 行     4, 9, 14, 3,  // 第 1 行     8, 13, 2, 7,  // 第 2 行     12, 1, 6, 11  // 第 3 行 };

shiftTab 数组的每个元素表示 ShiftRows 操作后的字节位置，例如，shiftTab[1] = 5 表示第 1 个字节在 ShiftRows 操作后移动到第 5 个字节的位置。该步骤在之前MixColumns时已经体现了，通过 shiftTab 数组，ShiftRows 操作已经被嵌入到查找表的生成过程中。关键代码如下：

1 2 3 4 5 6 7 8 9

for (int i = 0; i < 10; i++) {     for (int j = 0; j < 16; j++) {         int orgJ = shiftTab[j]; // ShiftRows 操作         u8 ioInv = ioInvTable[orgJ];         for (int x = 0; x < 256; x++) {           ...         }     } }

05. 实现加密能力

综合以上各个步骤的分析，我们来对比实现一下 AES-128 的加密流程，核心代码如下：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63

void AesBoxEncrypt() {     // 1. 初始化随机混淆表 ioInvTable     u8 ioInvTable[16] = {0}; // 用于存储随机生成的混淆数据     srand(time(nullptr));    // 设置随机种子     for (unsigned char &i : ioInvTable)     {         i = rand() % 256; // 生成 0-255 的随机数，填充到 ioInvTable 中     }       // 2. 生成 TyiTables 查找表，用于替换 MixColumns 操作     for (int j = 0; j < 4; j++) // 遍历每一列（共 4 列）     {         for (int x = 0; x < 256; x++) // 遍历每个可能的输入字节（0-255）         {             // 计算 TyiTables 的每个表项，包含 MixColumns 操作的结果             TyiTables[4 * j + 0][x] =                 ((gMul(2, x) ^ ioInvTable[4 * j + 0]) << 24) | (x << 16) | (x << 8) | gMul(3, x);             TyiTables[4 * j + 1][x] =                 (gMul(3, x) << 24) | ((gMul(2, x) ^ ioInvTable[4 * j + 1]) << 16) | (x << 8) | x;             TyiTables[4 * j + 2][x] =                 (x << 24) | (gMul(3, x) << 16) | ((gMul(2, x) ^ ioInvTable[4 * j + 2]) << 8) | x;             TyiTables[4 * j + 3][x] =                 (x << 24) | (x << 16) | (gMul(3, x) << 8) | gMul(2, x) ^ ioInvTable[4 * j + 3];         }     }       // 3. 生成 TBoxes 和 TyiTableBoxes 查找表，用于替换 SubBytes、AddRoundKey 和 MixColumns 操作     for (int i = 0; i < 10; i++) // 遍历每一轮（共 10 轮）     {         for (int j = 0; j < 16; j++) // 遍历每个字节（共 16 字节）         {             int shiftTab[16] = {                 0, 5, 10, 15, // ShiftRows 操作的字节位置映射                 4, 9, 14, 3,                 8, 13, 2, 7,                 12, 1, 6, 11};             int orgJ = shiftTab[j]; // 获取 ShiftRows 操作后的字节位置             u8 ioInv = ioInvTable[orgJ]; // 获取随机混淆数据             for (int x = 0; x < 256; x++) // 遍历每个可能的输入字节（0-255）             {                 u32 tmp = x;                 if (i != 0)                     tmp = tmp ^ ioInv; // 对输入进行随机混淆                 tmp = sBox[tmp ^ expandedKey[16 * i + orgJ]]; // 执行 SubBytes 和 AddRoundKey 操作                 TBoxes[i][j][x] = tmp; // 将结果存储到 TBoxes 中                 if (i == 9)                 {                     // 最后一轮不需要 MixColumns 操作，直接与轮密钥异或                     TBoxes[i][j][x] ^= expandedKey[160 + j];                 }                 else                 {                     // 其他轮需要执行 MixColumns 操作，结果存储到 TyiTableBoxes 中                     TyiTableBoxes[i][j][x] = TyiTables[j][tmp]; // MC0*(x0 ... x7)                 }             }         }     }       // 4. 对 TyiTableBoxes 进行混淆，增加攻击者逆向工程的难度    ... }

1. 初始化随机混淆表

• 功能: 生成一个随机字节数组 ioInvTable，用于对查找表的输入进行混淆。
• 实现:
  • 使用 srand(time(nullptr)) 设置随机种子。
  • 使用 rand() % 256 生成 0-255 的随机数，填充到 ioInvTable 中。

1. 生成 TyiTables 查找表

• 功能: 生成 TyiTables 查找表，用于替换 MixColumns 操作。
• 实现:
  • 遍历每一列（共 4 列）和每个可能的输入字节（0-255）。
  • 使用有限域乘法（gMul）计算 MixColumns 的结果，并将结果存储到 TyiTables 中。

1. 生成 TBoxes 和 TyiTableBoxes 查找表

• 功能: 生成 TBoxes 和 TyiTableBoxes 查找表，用于替换 SubBytes、AddRoundKey 和 MixColumns 操作。
• 实现:
  • 遍历每一轮（共 10 轮）、每个字节（共 16 字节）和每个可能的输入字节（0-255）。
  • 使用 shiftTab 数组实现 ShiftRows 操作。
  • 对输入进行随机混淆，并执行 SubBytes 和 AddRoundKey 操作，结果存储到 TBoxes 中。
  • 对于非最后一轮，执行 MixColumns 操作，结果存储到 TyiTableBoxes 中。

1. 对 TyiTableBoxes 进行混淆

• 功能: 对 TyiTableBoxes 进行异或混淆，增加攻击者逆向工程的难度。
• 实现:
  • 遍历每一轮（共 9 轮）、每一列（共 4 列）和每个可能的输入字节（0-255）。
  • 使用 MixTable 对 TyiTableBoxes 的每个表项进行异或混淆。

总结

希望以上内容能为您提供在 AES 白盒化的过程中的思路，如有错误或表述不当的地方请斧正，个人也在学习探索中，共勉。